More monadic art (fractal outtakes)

One fun thing about drawing with a computer is that you can make much more interesting mistakes than you can by hand. A human will quickly realize something is wrong with the algorithm and stop. But a computer will bravely repeat the same mistake, say, 8^6 times.

Here are a couple of my favorite “outtakes” from the monadic fractal project I’ve been blogging about recently.  Believe it or not, this was supposed to be the Sierpinski carpet:

There was a tiny typo in the function that replicates squares.  This is drawn entirely with quadrilaterals, though most are degenerate.  It was a bit shocking at first to see this output instead of the Sierpinski carpet I was expecting, but I quite like the simultaneously tousled and yet perfectly 4-fold rotationally symmetric look.

And then there’s this bunch of squares:

I miscalculated the scaling factor for the fractal I was trying to generate, and got squares that were just slightly too big.  Still, my incorrect scaling factor turned out to be an interesting one, and the overall effect is not bad.

I wonder what other art works out there started out by making interesting mistakes.

Fractals and Monads – Part 3

I promised more examples of using monads to draw fractals.  Let’s do some!

Today I’ll explain a simple method to draw lots of fractal pictures with minimal code, using the idea of Kleisli powers I introduced in the previous part. This will be easy to implement in Haskell, and accessible even if you’re not a Haskell programmer.

To do this, I’ll first introduce another well known way of drawing fractal pictures, using random motion.  If you haven’t seen this before, it’s cool in its own right, but then we’ll change the rules slightly and generate fractals instead using monads.  I’ll again be using the power set and list monads this time, so if you’ve read the first two parts, this should be familiar.

The Chaos Game

In the “Chaos Game” you pick a fixed set of affine transformations of the plane, usually all contraction mappings, and then watch what happens to a single point in the plane when you apply a randomly chosen sequence from our set of transformations.

For example, in the best-known version of this game we take just three transformations, each a scaling of the plane by a factor of 1/2, but each around a different fixed point. More precisely, fix points A, B, and C, the vertices of a triangle, and define three corresponding transformations 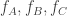by

Here’s how the game typically starts:

I’ve picked a random starting point and a random sequence which begins B, A, C, B, B, B, A, A, B, … .  You can see that at each step, we’re moving in a straight line half way to the next point in the sequence.

At first, it doesn’t sound doesn’t seem like anything very exciting is happening.  But if we keep going, we find something interesting.  To show the pattern more clearly, I’ll stop drawing the lines between steps, and just keep track of the successive points.  I’ll also shrink the dots a little, to avoid them running into each other.  Here’s what a typical random orbit looks like after 3000 iterations:

A picture of the Sierpinski triangle is already emerging.  After 10,000 iterations it looks like this:

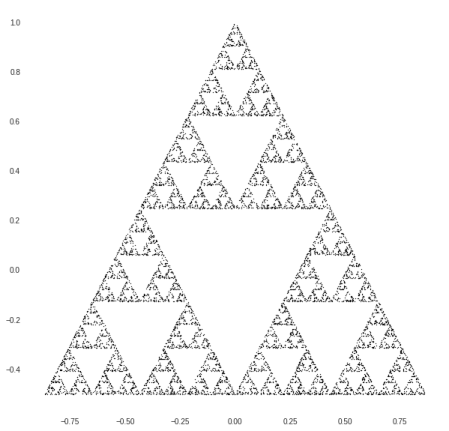
And after 50,000 iterations it’s getting quite clear:

There are tons of variations of the “chaos game,” which also go by the less flashy but more descriptive name of “Iterated Function Systems.”  But let’s get to the monads.

Removing the Randomness with Monads

What does the Chaos Game have to do with monads?  While it’s fun to generate fractal pictures using random motion, we can also trade this random process for a completely  deterministic one in which we iterate a single morphism in the Kleisli category of a monad.

In general, an alternative to making random selections between equally likely steps is to take all of the possible steps simultaneously.  That is, we can get rid of the randomness at the cost of replacing the ordinary functions with a multi-valued function.  Monads give us a nice way to handle this: we’ve seen before that multi-valued functions are just morphisms in the Kleisli category of the power set monad, and we can compose them using Kleisli composition.

In our case, the functions used in the chaos game are 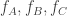, which move points closer to A, B, C, respectively.  We can combine these into a single function

given by

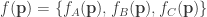
We then have only to iterate this.

The resulting code gives us pictures similar to the ones for the original chaos game, but much more regular and symmetric, since we’ve avoided making any random choices by making all possible choices.  If we also start out in a symmetric state, picking (0,0) as our starting point, and letting the fixed points A, B, and C form an equilateral triangle centered around this point, then at each generation thereafter we get a picture that has all of the symmetries of a triangle.

Here’s generation 6, with points:

Here’s generation 8, with 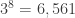points:

And here’s generation 10, with 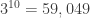points:

Comparing this to the picture from the chaos game with 50,0000 iterations, the two are very similar, though the “monadic” version has sharper edges, and none of the small scale noise of the random version.

The code

To implement this in Haskell, I need to define what a point in the plane is, and define a few operations on points.  I’ll define a new data type, Point, which really just consists of pairs of real (or more accurately, floating point) numbers, and I’ll define vector addition and scalar multiplication on these in the obvious way:

type Point = (Float,Float)

add :: Point -> Point -> Point
add (x1,y1) (x2,y2) = (x1+x2,y1+y2)

mult :: Float -> Point -> Point
mult r (x,y) = (r*x,r*y)

Sure, I could use a linear algebra library instead; I’m implementing these operations myself mainly because it’s easy, and perhaps more friendly and instructive for those new to Haskell.

Using these operations, we can build a function that scales the plane around a given point. I’ll do this more generally than in the examples above, because it will be useful for other versions of the chaos game which I’ll discuss later.  If is a point in the plane, and is a real number, then the function

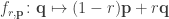
scales 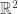by a factor around the point 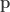. Here’s a Haskell implementation of this function:

scaleAround :: Float -> Point -> Point -> Point
scaleAround r p q = ((1-r) `mult` p) `add` (r `mult` q)

This can be read as saying we take two parameters, a real number r and a point p, and this results in a function from points to points, which is really just 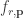.  The ` marks around add and mult let us use these as “infix” operators, as opposed to prefix operators like in Polish notation; for example 3 `mult` (1,0) means the same as mult 3 (1,0), and both give the result (3,0).

Now, we can make a list-valued function that will generate the Sierpinski triangle.  First, let’s fix the vertices of our triangle, which will just be a list of Points:

triVertices = [(sin(2*k*pi/3), cos(2*k*pi/3)) | k <- [0..2]]

This is so much like the mathematical notation for sets that it needs no explanation; just squint until the <- starts to look like , and remember that we’re dealing with Haskell lists here rather than sets.

As before, our function for generating this fractal combines all of the where 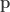ranges over the vertices in the triangle:

f :: Point -> [Point]
f q = [scaleAround 1/2 p q | p <- triVertices]

The first line is the type signature of the function; it just says f takes a point as input, and returns a list of points as output.  This is our morphism in the Kleisli category of the list monad.  The rest of the code just amounts to taking Kleisli powers of this morphism.  Recall that code from last time:

kpow :: Monad m => Int -> (a -> m a) -> a -> m a
kpow 0 _ = return
kpow n f = f <=< kpow (n-1) f

That’s everything we need.  Let’s pick our starting point in 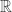to be the origin, set the number of generations to 10, and calculate the output data:

startPt = (0,0) :: Point
nGens = 10

outputData = kpow nGens f $ startPt

The last line here takes the 10th Kleisli power of f, and then applies that to the starting point (0,0). The result is the list of points, and if you plot those points, you get the picture I already posted above:

More examples

Once you know the trick, you can build new versions of the chaos game to generate other fractals.

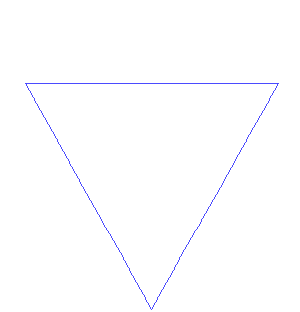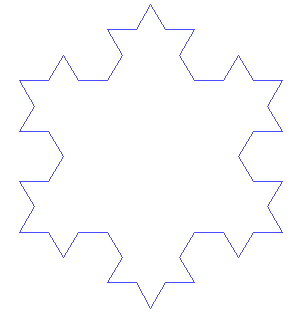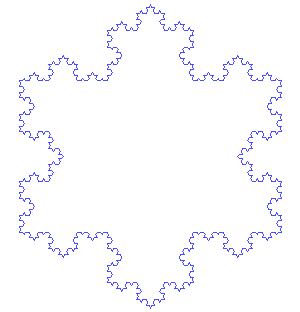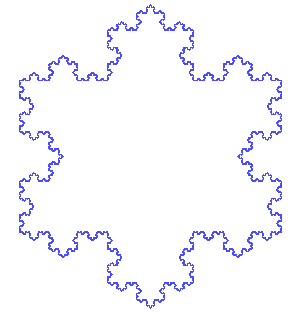
Here’s a fun one. Before, we started with an equilateral triangle and scaled around each of its vertices by a factor of 1/2; Now let’s take a regular hexagon and scale around each of its vertices by a factor of 1/3.

To build this using our monadic methods, all we really need to change in the code I’ve written above is which vertices and scaling factor we’re using:

hexVertices = [(sin(2*k*pi/6), cos(2*k*pi/6)) | k <- [0..5]]

f q = [scaleAround 1/3 p q | p <- hexVertices]

The result?

It’s a Koch curve!  Or rather, it’s lots of copies of the Koch curve at ever smaller scales. This is just the fractal that I’ve written about before, starting with “Fun with the Koch Snowflake” which I wrote when I first discovered it. It’s like a “Sierpinski Koch snowflake” because it can also be built by starting with a Koch snowflake and the repeatedly removing a Koch snowflake from the middle to leave six new Koch snowflakes behind.

The reason this slightly modified chaos game gives the Sierpinski Koch snowflake is essentially that, at each stage, the Koch snowflake splits into six new Koch snowflakes, each a third of the size of the original, and distributed in a hexagonal pattern.

How does this generalize?  There’s a whole family of fractals like this, which I posted about before, and there’s a version of the chaos game for each one.

I explained in Fun with the Koch snowflake how this replication rule for triangles:

leads to the Sierpinski Koch Snowflake we found above:

Similarly, I explained how this replication rule for squares:

leads to an analogous fractal with octagonal symmetry:

and how this replication rule for pentagons:

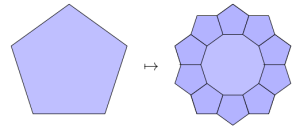
leads to this:

fractal with decagonal symmetry.  This sequence continues.

To get the transformations needed for the chaos game, we just need to calculate how much smaller the polygons get in each successive generation. If you stare at the replication rules above, you can see that pattern I’m using: the edge of the parent polygon is congruent to two edges of the child polygon plus a segment extending from one vertex to the next-to-adjacent vertex of the child polygon.  Solving this, the correct scaling factor is

.

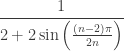The chaos game—and the tamer “monadic” variant on it—for these fractals just amounts to scaling by this factor around each of the vertices in a regular 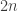-gon.

By the way, you might be tempted (I was!) to include some rotations in addition to the scale transformations, since in the polygon-based versions, only half of the polygons have the same angular orientation as their parent.  However, these rotations turn out not to matter when we’re using points as our basic geometric objects rather than polygons.

Again, there’s little code we need to modify.  First, since we need polygons with any number of sides, let’s make a function that takes an integer and gives us that many vertices distributed around the unit circle, with the first vertex always at 12 O’Clock:

polyVertices :: Int -> [Point]
polyVertices n = [(sin(2*k*pi/nn), cos(2*k*pi/nn)) | k <- [0..(nn-1)]]
    where nn = fromIntegral n

If you’re new to Haskell, this should all be familiar by now, except perhaps the last line. Haskell will complain if you try dividing a floating point number by an integer since the types don’t match, so the integer n has to be converted to a float nn; this makes k also a float, since the notation [0..x] actually means the list of all of the floating point integers from 0 to x, if x is a floating point number, and then everything in sight is a float, so the compiler is happy.

We then have to change our generating morphism to:

f :: Int -> Point -> [Point]
f n q = [scaleAround r p q | p <- polyVertices (2*n)]
    where r = 1/(2 + 2*sin((nn-2)*pi/(2*nn)))
          nn = fromIntegral n

and remember that the generating morphism is now not just f but f n.

Now we can set the starting point, the number of “sides” of the basic polygon, and the number of generations, as we wish:

startPt = (0.2,0.5) :: Point 
m = 5               -- number of generations
n = 7               -- number of "sides"

outputData = kpow m (f n) $ startPt

Just remember that the final list is a list of 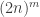points, so don’t blame me if you make these numbers big and run out of memory. :-)

In any case, with code like this, you can generate analogs of the Sierpinski Koch snowflake based on squares:

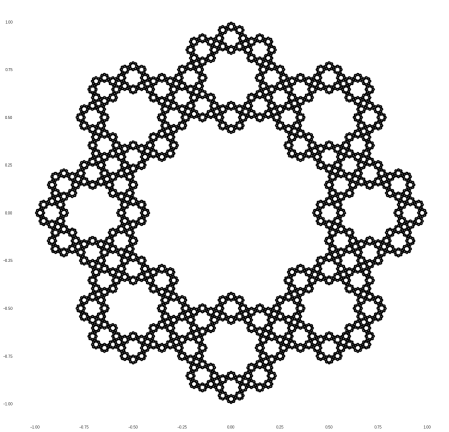
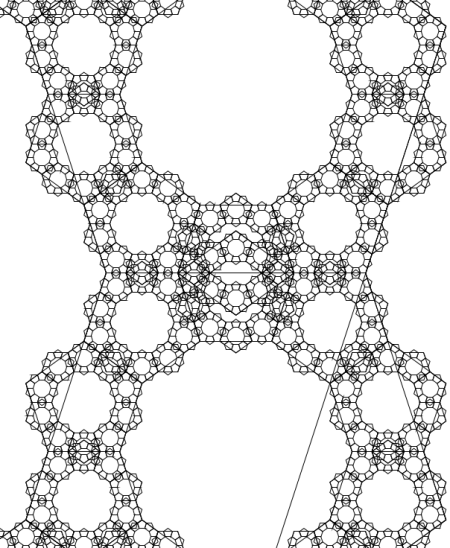
Pentagons, which start “overlapping”:

Hexagons, where the overlapping becomes perfect:

and more.  Heptagons, where the overlapping gets a bit more severe:

Octagons:

and so on.

But enough of that.  Next time, I’ll move on to fractals of a different sort …

Fractals and Monads – Part 2

Last time I discussed the power set monad and how it shows up in certain methods of building fractals.  This time I’ll go a bit further, and also explain some Haskell code I actually use to generate fractal pictures like this:

To do this, I’ll introduce Kleisli categories, the list monad, and a bit about how monads work in Haskell!

Recall we were considering fractals that can be built using a “replication” function

on some set of “shapes” .  As an example, we had considered a map that takes any triangle in the plane to sets of three new triangles as shown here:

and we noted that “iterating” this map indefinitely gives us all of the triangular “holes” in a Sierpinski triangle:

I also described how iterating this map, if we do everything carefully, involves the structure of the power set monad.

In fact, considering maps like leads us directly to the “Kleisli category” associated to the power set monad.  I want to explain this here, because in computer science people actually tend to think of monads essentially in terms of their associated Kleisi categories, and that’s how monads are implemented in Haskell.

Every monad has an associated Kleisli category, but since I’ve been working with the power set monad in the category of sets, I’ll start with that special case.

First, in the Kleisli category, which we’ll denote , the objects are the same as the original category : they’re just sets.  A morphism from the set to the set , however, is a function

For now, at least, I’ll avoid making up any special notation for morphisms in the Kleisli category, and instead freely regard either as a morphism from to in the category of sets, or as a morphism from to in the Kleisli category ; these are really the same thing.  If this is confusing, whenever you’re thinking of as a morphism in the Kleisli category, just think of the as decoration on the arrow , rather than on the codomain object .

Given two functions and , the Kleisli composite is defined by

Checking the domain and codomain of each of the functions on the right, we can see that this indeed gives a morphism from to in the Kleisli category:

You can check that is associative, and that the maps are identity morphisms, so we really do get a category. That’s all there is to the Kleisli category.

Returning to the sort of function we had been considering for generating fractals:

these are clearly just endomorphisms in the Kleisli category.  This also makes it clear what we mean by “iterating” such a function: it’s an endomorphism, so we can just compose it with itself as many times as we want.  In particular, analogously to how we define “powers” of ordinary functions by repeated composition, we can define the nth Kleisli power of recursively by

That is, the 0th power of is the identity, while the nth power of is the Kleisli composite of with its (n-1)st power.

For example, consider the set of all equilateral triangles in the plane and consider the map defined so that has six elements, each 1/3 the size of, and linked together around the boundary of the original triangle , as shown here:

Then, starting with an arbitrary triangle the images under successive Kleisli powers of the generating endomorphism:

look like this:

Some Haskell

Let’s do some Haskell—If you don’t know Haskell, don’t worry; I’ll explain what everything means. If you do know Haskell, this will be super easy, perhaps even obvious, though I may write things in ways you won’t expect, since I’m transitioning over from the categorical definition of monad, rather than diving in with how monads are actually defined in Haskell.

The code we really need is almost embarrassingly short, mainly because monads are extremely well suited to the task at hand.  What we need most is just to be able to compute Kleisli powers!

Here’s how the formula for the Kleisli power of an endomorphism becomes a function in Haskell:

import Control.Monad

kpow :: Monad m => Int -> (a -> m a) -> a -> m a
kpow 0 _ = return
kpow n f = f <=< kpow (n-1) f

Let’s go through this line by line.

The first line just loads some tools for working with monads; there’s not much I need to say about that now.

The next line is the first one of real content; it’s the “type signature” of the function “kpow”.  The first bit, Monad m, just says that m is any monad; Haskell knows about several monads, and you can also define your own.   Then, the rest of that line:

Int -> (a -> m a) -> a -> m a

can be interpreted as declaring that we have a function that takes one integer (Int), the “power,” and one element of , (i.e. something of type a -> m a), and gives us another element of .  So if I were to write this line in standard mathematical notation, I would write:

where is any monad, and is any type.  We take an integer and a Kleisli endomorphism for the monad m, and return another endomorphism. Notice there’s a slight discrepancy here, in that an Int is any integer, whereas I used the natural numbers .  But the integer really is intended to be non-negative.  If you fed a negative integer into kpow, the recursion would never terminate; so, my code doesn’t forbid it, but you shouldn’t do it.

The last two lines of the code give the actual formula for the Kleisli power. If you just look at my earlier formula:

and compare this to these two lines:

kpow 0 _ = return
kpow n f = f <=< kpow (n-1) f

you can probably figure out all of the Haskell syntax just by matching up symbols.

The first line says “whenever the first argument of kpow is 0, the result is “return.” This may be confusing if you’re used to how the keyword “return” is used in many other programming languages. Sorry; it’s not my fault! In Haskell “return” means “ for any object “, where the objects in this case are always data types.

The second line says “the nth Kleisli power of f is the composite of f with the (n-1)st power of f”, just as in the other formula. You probably guessed that the Kleisli composite is written f <=< g in Haskell.

Here’s a dictionary relating the notation I’ve been using to Haskell notation for the same thing:

I didn’t need to use , a.k.a. join explicitly in the definition of Kleisli powers, since it’s already wrapped into the definition of Kleisli composition.

List monad

To do some examples I’ll use the list monad, which is a built-in monad in Haskell. This is very much like the power set monad, since “lists” are like sets in many ways, so I can introduce this pretty quickly. We really just need a very basic idea of how the list monad works.

A “list” of elements of “type” can be written written simply as

for a finite list, or for an infinite list.

Making lists of elements of a given type clearly gives a functor analogous to the power set functor: for any function we get a function that just acts element-wise on lists:

mapping a list of elements of type into a list of elements of type .

Based on what we’ve done with sets, you can probably guess how the two natural transformations in the list monad work, too.

First, any single item can be regarded as a list with only one item on it, so

In Haskell, for example, you could take an element of type Int, say the integer 5, and turn it into a list of integers by using return 5. As long as Haskell has a context to know it is working in the list monad rather than some other monad, this will output [5]. Voilà!

Second, the natural transformation turns lists of lists into lists.  If you’ve got a list of to-do lists, you can always turn it into a single list by first writing down the items on the first list, in order, then continuing with the items on the second list, and so on.

In Haskell, If you enter join [[1,2,3],[4,5]], you’ll get [1,2,3,4,5] as output. That’s .

There’s one noteworthy subtlety, which is that infinite lists are also allowed. So, if you have a list of lists:

[Fun stuff to do, Work to do]

and the first item happens to be an infinite list, then if you try joining these lists up into one in the way I described, you’ll never get to any items on the second list. This is one way in the list monad differs from in the power set monad: In the former, as soon as one of the lists is infinite, everything after that gets thrown away. This last part is not obvious; you certainly could devise ways to join a list of infinite lists together and include all of the items, but that’s not how things work in this monad.

You can easily work out how Kleisli composition works from this, so we’ve now got everything we need.

Cantor set in the List Monad.

Let’s do an example: the Cantor set. I’ll represent closed intervals on the real line by ordered pairs in Haskell. So, when I write (0.3, 1.5), I mean the set . I know, round brackets for closed intervals is weirdly non-standard, but in Haskell, square brackets are reserved for lists, and it’s better to keep things straight.

To generate the Cantor set, all we need is the Kleisli endomorphism in the list monad that describes the general step. This can be defined by a one-line Haskell function:

f (p,q) = [(p, p + (q-p)/3), (q-(q-p)/3, q)]

If we apply this to the unit interval (0, 1), here’s what we get:

[(0.0,0.3333333333333333),(0.6666666666666667,1.0)]

So this works: it’s mapping the closed interval to a list of two closed intervals: and .

Now we can compute any step in the construction of the Cantor set by computing Kleisli powers. Let’s just do one. Once you’ve loaded the function kpow, enter this in Haskell:

kpow 3 f (0,1)

and—kapow!—you’ll get this output:

[(0.0,3.7037037037037035e-2),
 (7.407407407407407e-2,0.1111111111111111), 
 (0.2222222222222222,0.25925925925925924),
 (0.2962962962962963,0.3333333333333333),
 (0.6666666666666667,0.7037037037037037),
 (0.7407407407407408,0.7777777777777778),
 (0.888888888888889,0.9259259259259259),
 (0.962962962962963,1.0)]

Ugly isn’t it? But convert to fractions and you’ll see this is doing just the right thing.

I’ll do more examples in the next post.

Fractals and Monads — Part 1

A while back, I posted a bunch of fractal artwork that I did for fun, based on variations of the Koch snowflake; like this one, for example:

This is composed entirely of equilateral triangles, but it’s just one step in an iterated process leading to a fractal consisting of infinitely many Koch snowflakes at ever smaller scales.

I had a lot of fun coming up with designs like this, but actually I didn’t start out wanting to do new things with the Koch snowflake—that was just a fun tangent.  Originally, I was thinking about monads!

It’s high time I got back to what I was originally working on and explained what these fractals have to do with the “power set monad.”  To do that, I should probably start by explaining what the power set monad is.

For any set the power set is the set of all its subsets.  If you’ve ever studied any set theory, this should be familiar.  Unfortunately, a typical first course in set theory may not go into the how power sets interact with functions; this is what the “monad” structure of power sets is all about. This structure has three parts, each corresponding to a very common and important mathematical construction, but also so simple enough that we often use it without even thinking about it.

Let me finally say what the monad structure of power sets actually is.

First, mapping sets to their power sets is actually a functor:  For any function , there corresponds a function

which sends each element , i.e. each subset , to its image:

.

This makes a functor because the mapping of functions gets along nicely with identity functions and composition.   This functor is the first part of the power set monad.

You might be accustomed to writing the image of the set under simply as , rather than .  But here, we need to be more careful: despite its frequent use in mathematics,  is a notational abuse for which is the proper form.

To motivate the next piece in the power set monad, notice that there’s a strong sense in which is just an extension of , namely, on singleton sets, it essentially “is” :

.

This might make it tempting write for , as sort of “dual” version of the previous abuse of notation, though I don’t think anyone does that.

A better way to express how extends is to introduce the canonical map sending elements of to the corresponding singleton sets:

Then, the previous equation can be written , which is precisely the equation that makes a natural transformation. This natural transformation is the second piece in the monad structure.

Anyone who’s taught elementary set theory can attest that some students have a hard time at first making with conceptual distinction between elements and singleton subsets of a set.  Indeed, conflating the two is a very “natural” thing to do, which is why this is a natural transformation.

The last piece of the power set monad is another natural transformation. Much like , which formalizes a way to think of elements as being subsets, there is a natural transformation that lets us think of sets of subsets as being subsets.  This is given by, for each set , a map:

Here is the power set of the power set of , so an element of it is a sets of subsets of , and we turn this into a single subset by taking the union.

That’s it!  Or, almost.  To form a monad, the data must be compatible in such a way that these diagrams commute:

It’s a simple exercise to check that this is indeed the case.  You can extract the general definition of monad from what I’ve written here: you need an endofunctor on some category, and two natural transformations such that the diagrams analogous to those above commute.

Now let’s come back to fractals:

Many kinds of fractals are created by taking a simple shape, making multiple copies, transforming them somehow—for example, by shrinking or rotating—and then repeating.

For example, here’s one way to build a Sierpinski triangle, or rather its complement, staring from a single triangle and a rule for how triangles should “reproduce”:

If we look closely, we see that this process naturally involves ingredients from the power set monad.

In particular, the basic building block is the self-replication rule that we can write as a function

where is the set of triangles in the plane.  We won’t need an explicit formula for the function, since a picture suffices to explain what it does:

We can get all of the triangular holes in the Sierpinski triangle by “iterating” f. But, what does this mean exactly?  It would be nice if we could just do , but, strictly speaking, this doesn’t parse: we can’t feed a set of triangles into , since this is a function that expects a single triangle as input.

Fortunately, we know the solution to this problem: since , we can’t feed it into , but we can feed it into .  Good so far.

The problem with this is that again doesn’t live in , nor does it live in —it lives in :

It seems we would be doomed to march into ever more deeply-nested sets, were it not for the natural transformation .  Fortunately, using we get

So, now we can see the process of building a fractal as just repeatedly applying this function .

One last problem: What do we apply it to?  We want to apply it to our initial triangle , but that’s an element of , not .  Good thing we can think of this as an element of using the natural transformation !

So, here’s a recipe to build a wide variety of fractals, like some of the ones I’ve posted on this blog:

but also tons of others, using the power set monad:

1. Start with a replication rule on some set of “shapes.”
2. Pick a shape .
3. Feed your initial shape into to get the initial state.
4. Iterate feeding the current state into to get a new state, as many times as you want.

In fact, in calling this a “recipe,” I mean more than just an abstract mathematical recipe: this is essentially how I really drew all of those fractal pictures.  I generated them using Haskell—a functional programming language that knows about monads.  I didn’t use the power set monad, but rather Haskell’s built in “list monad,” which works very similarly.

3d Fractal models

My student Colton Baumler has been printing 3d versions of some of the fractal designs I posted about a few months ago:

That’s his three-dimensional interpretation of the first few iterations of this design of mine:

What’s fun about Colton’s version is that each new layer of squares is printed a bit taller than the previous layer.  I had really only imagined these as two-dimensional objects, so for me it’s really fun to have 3-dimensional models of them to hold and play with!  Colton’s idea of adding some depth really adds another … er … dimension to the overall effect:

His work also gives a nice way to illustrate some of the features of these fractals.  For example, visually proving that the “inside” and “outside” in my fractals converge to the same shape can be done by printing the same model at different scales.  Here are three copies of the same fractal at different scales, each printed with the same number of iterations:

Not only do these nest tightly inside each other, the thickness is also scaled down by the same ratio, so that the upper surfaces of each layer are completely flush.

Colton has been doing this work partly because designing fractals is a great way to learn 3d printing, and he’s now getting some impressively accurate prints.  But, I also like some of his earlier rough drafts.  For example, in his first attempt with this fractal based on triangles:

there were small gaps between the triangles, which Colton hadn’t intended.  But, this gave the piece a sort of rough, edgy look that I like, and it casts shadows like castle battlements:

Colton is still doing nice new work, and we’ll eventually post some more pictures here. But I couldn’t wait to post a preview of some of his stuff!

(Designs and photos © 2018 Colton Baumler and Derek Wise)

A decagonal snowflake from pentagons

So far in these posts about fractals, I’ve shown (1) how letting triangles reproduce like this:

generates a bunch of copes of the Koch snowflake at different scales:

Similarly, I’ve shown (2) how letting squares reproduce like this:

generates a bunch of copies of a fractal related to the Koch snowflake, but with 8-fold symmetry:

So what about letting pentagons reproduce?   For pentagons, an analog of the replication rules above is this:

Each of the 10 cute little pentagon children here is a factor of smaller than its parent, where is the golden ratio.

However, something interesting happens here that didn’t happen with the triangle and square rules. While triangles and squares overlap with their ancestors, pentagons overlap with both their ancestors and their cousins.  The trouble is that certain siblings already share faces (I know, the accidental metaphors here are getting troublesome too!), and so siblings’ children have to fight over territory:

In this three-generation pentagon family portrait, you can see that each second generation pentagon has two children that overlap with a cousin.

As we carry this process further, we get additional collisions between second cousins, third cousins, and so on.  At five generations of pentagons, we start seeing some interestingly complex behavior develop from these collisions:

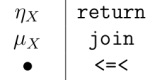
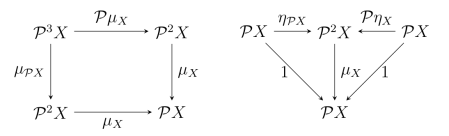
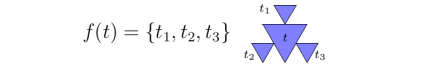
There’s a lot of fascinating structure here, and much of it is directly analogous to the 6-fold and 8-fold cases above, but there are also some differences, stemming from the “cousin rivalry” that goes on in pentagon society.

Let’s zoom in to see some collisions near where the two ‘wreaths’ meet on the right side of the picture:

I find the complicated behavior at the collisions quite pretty, but the ordering issues (i.e. which members of a given generation to draw first when they overlap) annoy me somewhat, since they break the otherwise perfect decagonal symmetry of the picture.

If I were doing this for purely artistic purposes, I’d try resolving the drawing order issues to restore as much symmetry as possible. Of course, I could also cheat and restore symmetry completely by not filling in the pentagons, so that you can’t tell which ones I drew first:

It’s cool seeing all the layers at once in this way, and it shows just how complex the overlaps can start getting after a few generations.

Anyway, because of these collisions, we don’t get seem to get a fractal tiling of the plane—at least, not like we got in the previous cases, where the plane simply keeps getting further subdivided into regions that converge to tiles of the same shape at different scales.

Actually, though, we still might get a fractal tiling of the plane, if the total area of overlap of nth generation pentagons shrinks to zero as n goes to infinity!  That would be cool.  But, I don’t know yet.

In any case, the picture generated by pentagons is in many ways very similar to the pictures generated by triangles and squares. Most importantly, all of the similar-looking octagonal flower shaped regions we see in this picture including the outer perimeter, the inner light-blue region, and tons of smaller ones:

really are converging to the same shape,  my proposal for the 10-fold rotationally symmetric analog of the Koch snowflake:

How do we know that all of these shapes are converging to the same fractal, up to rescaling?  We can get a nice visual proof by starting with two pentagons, one rotated and scaled down from the other, and then setting our replication algorithm loose on both of them:

Proof:

We see that the area between the two fractal curves in the middle shrinks closer to zero with each generation.

Puzzle for Golden Ratio Fans: What is the exact value of the scaling factor relating the two initial pentagons?

Next up in this infinite series of articles: hexagons!  …

I’m joking!  But, it’s fairly clear we can keep ascending this ladder to get analogs of the Koch snowflake generated by n-gons, with (2n)-fold rotational symmetry.  More nice features might be sacrificed as we go up; in the case generated by hexagons, we’d have collisions not only between cousins, but already between siblings.

More fractal fun

In the previous article, I explained how the famous Koch snowflake can be built in a different way, using “self-replicating” triangles. This was a revelation for me, because I had always thought of the Koch snowflake as fundamentally different from other kinds of fractals like the Sierpinski triangle, and now I think of them as being basically the same.

In the Sierpinski triangle, each triangle yields three new, scaled-down triangles, attached at the midpoints of sides of the original, like this:

These triangles are usually thought of as “holes” cut out of a big triangle, but all I care about here is the pattern of the triangles.  As I explained last time, the Koch snowflake can be built in a similar way, where each triangle produces six new ones, like this:

You might say this bends the usual rules for making fractals since some of the triangles overlap with their ancestors.  But, it makes me happy because it lets me think of the Sierpinski triangle and the Koch snowflake as essentially the same kind of thing, just with different self-replication rules.

What other fractals can we build in this way?  The Sierpinski carpet is very similar to the Sierpinski triangle, where we now start with squares and a rule for how a square produces 8 smaller ones:

This made me wonder if I could generalize my construction of the Koch snowflake using triangles to generate some other fractal using squares.  In other words, is there some Koch snowflake-like fractal that is analogous to the ordinary Koch snowflake in the same way that the Sierpinski carpet is analogous to the Sierpinki traingle?

There is!  Taken to the 5th generation, it looks like this:

The outline of this fractal is an analog of the Koch snowflake, but with 8-fold symmetry, rather than 6-fold.  Compare the original Koch snowflake with this one:

Just as I explained last time for the Koch snowflake (left), the blue picture above actually provides a proof that the plane can be tiled with copies of tiles like the one on the right, with various sizes—though in this case, you can’t do it with just two sizes of tiles; it takes infinitely many different sizes!  In fact, this tiling of the plane is also given in Aidan Burns’ paper I referenced in the previous post.

But, my construction is built entirely out of self-replicating squares.  What’s the rule for how squares replicate?

Before I tell you, I’ll give two hints:

First, each square produces 8 new squares, just like in the Sierpinski carpet.  (So, we could actually make a cool animation of this fractal morphing into the Sierpinski carpet!)

Second, you can more easily see some of the bigger squares in the picture if you make the colors of the layers more distinct.  While I like the subtle effect of making each successive generation a slightly darker shade of blue, playing with the color scheme on this picture is fun.  And I learned something interesting when my 7-year old (who is more fond of bold color statements) designed this scheme:

The colors here are not all chosen independently; the only choice is the color of each generation of squares.  And this lets us see bits of earlier-generation squares peeking through in places I hadn’t noticed with my more conservative color choices.

For example, surrounding the big light blue flower in the middle, there are 8 small light blue flowers, and 16 even smaller ones (which just look like octagons here, since I’ve only gone to the 5th generation); these are really all part of the same light-blue square that’s hiding behind everything else.

The same thing happens with the pink squares, and so on.  If you stare at this picture, you can start seeing the outlines of the squares.

So what’s the rule?  Here it is:

Fun with the Koch snowflake

I was playing with fractals recently and discovered a fun way to construct the Koch snowflake. It may not be new to the world, given how much is known about fractals, but it was new to me. In any case, it’s really cool!  It lets you see a lot more interesting self-similarity in this fractal, and effortlessly leads to the known tilings of the plane by Koch snowflakes.

The  Koch snowflake is usually constructed starting with an equilateral triangle by replacing the middle third of each side with an equilateral triangular protrusion, doing this again to the resulting polygon, and so on.  The first seven steps are shown in this animation:

and the Koch snowflake is the “limit” of this process as the number of steps goes to infinity.

In the alternative construction we use only self-replicating triangles.  We again start with a triangle:

But now, rather than modifying this triangle, we let it “reproduce,” yielding  six new triangles, three at the corners of the original, and three sticking out from the sides of the original.  I’ll make the six offspring a bit darker than the original so that you can see them all:

Notice that three of the children hide the corners of their parent triangle, so it looks like we now have a hexagon in the middle, but really we’ve got one big triangle behind six smaller ones.  Now we do the same thing again, letting each of the six smaller triangles reproduce in the same way:

The 36 small triangles are the “grandchildren” of the original triangle; if each of these has six children of its own, we get:

Repeating this again:

  And again:

At this stage, it starts getting hard to see the new triangles, so I’ll stop and rely on your imagination of this process continuing indefinitely.  We can now see some interesting features emerging.  Here are some of the main ones:

1. The outer perimeter of all of these triangles, taken to the infinite limit, is the Koch snowflake.
2. The lightest blue region, in the middle, is also converging to a smaller Koch snowflake, rotated from the outer one by .
3. Between the outer perimeter and the Koch snowflake in the middle are six more yet smaller Koch snowflakes.
4. The regions in the middle of these snowflakes are also Koch snowflakes …

and so on: we have Koch snowflakes repeating at smaller and smaller scales.

All this self similarity shows in particular that Koch snowflakes can be assembled out of Koch snowflakes.  This is nothing new; it’s related to Aidan Burns’ nice demonstration that Koch snowflakes can be used to tile the plane, but only if we use snowflakes of at least two different sizes:

Aidan Burns, Fractal tilings. Mathematical Gazette 78 No. 482 (1994) 193–196.

These tilings are already visible in the above construction using triangles, but we can make them even more evident by just playing with the color scheme.

First, if we draw the previous picture again but make all of the triangles the same color, we just get a region whose perimeter is the usual Koch snowflake:

On the other hand, if we make the original triangle white, but all of its descendants the same color of blue, we get this:

I hope you see how this forms part of a wallpaper pattern that could be extended in all directions, adding more blue snowflakes that bound larger white snowflake-shaped gaps. This gives the tiling of the plane by Koch snowflakes of two different sizes.

Taking this further, if we make the the original triangle and all of its children white, but all of their further descendants the same color of blue, we get this:

The pattern seen here can be extended in a hopefully obvious way to tile the whole plane with Koch snowflakes of three different sizes.

Going further, if we make the first three generations white, but all blue after that, we get:

and so on.

The previous four pictures are generated with exactly the same code—we’re drawing exactly the same triangles, and only changing the color scheme.  If we keep repeating this process, we get a tiling with arbitrarily small Koch snowflakes!

But we can also go the other way, continuing up in scale to get a tiling that includes arbitrarily large Koch snowflakes.  To do this, we just need to view the above series of pictures in a different way!

The way I described it, the scale is the same in all of the previous four pictures.   Making successive generations white, one generation at a time, makes it look as if we’re cutting out a snowflake from the middle of a big snowflake, leaving six similar snowflakes behind, and then iterating this:

On the other hand, we can alternatively view these pictures as a process of zooming out: each picture is built from six copies of the previous one, and we can imagine zooming out so that each picture becomes just one small piece of the next.

 

If you’re careful about how you do this, you get a tiling of the whole plane, with arbitrarily large Koch-snowflake shaped tiles!  I say you have to be careful because it won’t cover the whole plane if, for example, each picture becomes the top middle part of the next picture.  But, if you zoom out in a “spiral,” rotating by at each step, you’ll get a tessellation of the plane.

Someone should make an animation that shows how this works.  Maybe I’ll get a student to do it.

There are some other fun variations on this theme—including a similar construction that leads to the other “fractal tiling” described by Aidan Burns—which I should explain in another post.

In case anyone wants it, here is a 1-page visual explanation of the construction described in this post: snowflake.pdf

(All images in this post, except for the first, copyright 2017 Derek Wise.)