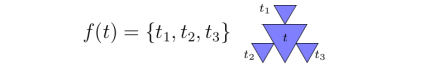More monadic art (fractal outtakes)

One fun thing about drawing with a computer is that you can make much more interesting mistakes than you can by hand. A human will quickly realize something is wrong with the algorithm and stop. But a computer will bravely repeat the same mistake, say, 8^6 times.

Here are a couple of my favorite “outtakes” from the monadic fractal project I’ve been blogging about recently.  Believe it or not, this was supposed to be the Sierpinski carpet:

There was a tiny typo in the function that replicates squares.  This is drawn entirely with quadrilaterals, though most are degenerate.  It was a bit shocking at first to see this output instead of the Sierpinski carpet I was expecting, but I quite like the simultaneously tousled and yet perfectly 4-fold rotationally symmetric look.

And then there’s this bunch of squares:

I miscalculated the scaling factor for the fractal I was trying to generate, and got squares that were just slightly too big.  Still, my incorrect scaling factor turned out to be an interesting one, and the overall effect is not bad.

I wonder what other art works out there started out by making interesting mistakes.

Discrete robot motion planning in a continuous domain

A robot has a discrete configuration space if it has a discrete set of possible actions at each step, right?

Wrong! In fact, even in a perfectly idealized world where there is zero error in motion, a robot with only discrete actions can effectively reach a continuum of different configurations. This can make motion planning for such robots very interesting.

Here’s a robot I built when I was about 15 years old:

I don’t have this robot anymore.  I gave it to the local jawas in the California desert before moving to Germany.   But now, a weekend’s worth of programming let me bring it back to life in a virtual world.  Plus, I’ve made it more intelligent than it ever was in its previous life.  Bwahhh-ha-ha!

Let me explain what’s interesting about this robot, and why I coded it into a virtual world.

The original robot could not do much.  It could rotate and move forward or backward only in fixed increments, and I could pre-program a sequence of moves ahead of time, which it would then execute.  I know—not very impressive as robots go these days.

But the limitations of this robot are also what make it interesting.  Since it only had discrete motions, and rather coarse ones at that, getting it to move from one location to another without running into things was an interesting challenge!

An ideal discrete robot

Let’s consider an idealized version of this robot which can do only two things:

1. Move forward or backward by exactly 1 meter.
2. Rotate in place in increments of exactly 45 degrees.

The robot I built was very much like this, although it moved some shorter distance (1m is just for a convenient number), and of course executed neither of the two possible moves with perfect consistency or accuracy. Still, it was rather good at doing what it was designed to.

In fact, we can idealize this robot just a bit more.  Let’s ignore the need for the robot to rotate and just assume it can move instantly in any of eight directions, each separated from 45 from the last.   Thus, if we point the robot Northward, at each stage it can move in any of eight basic compass directions: N, S, E, W, NW, NE, SE, and SW.

In a wide open space with nothing to run into, if you give our idealized robot a pen (like the Logo turtle) and send it out on a random walk, you’ll see something like this:

There’s something important to observe here: the locations where the robot stopped between moves, denoted by dots, can end up being very close together, even though the robot always moves in steps of one meter.

In fact, the robot can get essentially anywhere. The positions the robot can get to form a dense subset of the plane:  Given enough moves, it can stop as close as you wish to any destination point you pick.  I say it can “stop” close to the destination because I don’t want to count it is reaching its destination if it just rolls over the destination in transit without actually stopping there.  That would be cheating!

For example, suppose the robot is at (0, 0) and you want to program it to get to (0, 0.5).  Just telling the robot to move straight toward (0, 0.5) won’t work: it will drive through the point (0, 0.5), but it won’t stop there; it will keep going all the way to (0, 1).  In fact, you’ll never be able to reach (0, 0.5) exactly, but if you’re satisfied with getting there to within 0.1 meters of the destination, then there’s an easy solution with only 3 steps:

The red x marks the goal at (0, 0.5), and the final resting spot of the robot, marked by a red dot •, is within 0.1 of this.  More precisely, it’s easy to see that the robot comes to rest at the point , or approximately (0, 0.4142), which is within our acceptable error of 0.1 m.

If we’re not satisfied getting within 0.1 m, and we’d rather get within, say, 0.05 m (5cm) of the goal, we can still do it with a bit more thought.  Here’s a way to do it with 20 moves, not counting rotations:

Of course, solutions are not at all unique: Here are two more solutions to the same problem:

However, each of these also consists of 20 moves.  In fact, these are all minimal solutions: every solutions to this problem, at the specified precision of 5cm, has at least 20 moves not counting rotations.

Of course, you could also demand even more precision.  If you want to get from (0, 0) to (0, 0.5) to within a distance of 0.01, i.e. within 1cm, given our step size of 1m, you’ll need at least 119 moves:

Yikes!

Finding a plan to get from one location to another is an example of “motion planning” in robotics, and doing this kind of motion planning is one of the ways I had fun with the original robot when I was a teenager.  I learned to do some of this intuitively just by getting a feel for how to use combinations of moves.  Of course, that kind of intuition never let me do anything so complicated as finding the 119 moves above!

Motion planning on a hypercube lattice

The virtual reincarnation of my old robot, despite the disadvantage of lacking any corporeal existence, has one big advantage over its former self: it can solve the motion planning problem itself.

To  do this, it uses a classic AI tool—A* search.  This is an algorithm for finding minimal paths through weighted graphs, and is commonly used for route finding in map programs, solving puzzles, and planning complex sequences of actions.

In the robot’s case, although it occupies a 2d world which we identify with a subset of , the A* search is carried out instead on the 4-dimensional lattice representing the four directions it can travel in the physical space: the N-S, E-W, NE-SW, and SE-NW directions.

In other words, the robot really thinks of itself as living on a hypercube lattice.  You may be used to seeing pictures of hypercubes in one of their 3d projections, like this:

However, if you project a hypercube down into two dimensions in such a way that all of the edges have the same length in the projection, you can get this:

This picture of a hypercube is something I could draw with my robot!  All of the angles are multiples of 45 degrees, and all of the edges have the same length.  (Plus, I can draw it in one pass: all of the vertices are even, so there exists an Euler circuit.)

Of course, there’s a deep reason for this: the real configuration space of the robot, still ignoring the robot’s orientation, is a projection of a hypercube lattice into .  The vertices of this lattice are the states the robot can occupy at rest, while the edges represent the moves, or allowed transitions between states.

The entire hypercube lattice is like an ordinary cubical lattice:

but one dimension higher, and instead of 8 cubes meeting at each vertex, it has 16 hypercubes meeting at each vertex.  This is rather complicated to draw, and I won’t show a picture of the hypercube lattice.  However, for your amazement, here is a picture I drew of its projection into two dimensions:

There’s nothing wrong with this picture—The lattice’s projection is dense in , as my robot shows, remember! :-)

Explicitly, the basic projection can be written

where

The eight possible moves—or in other words, the edges in the hypercube lattice—correspond to incrementing or decrementing one of the coordinates $m, n, a, b$.  You can check that these project exactly to the eight allowed robot motions.

I combine this projection into with a translation and rotation, so that the robot’s current position in the lattice is always (0,0,0,0).

A* Search implementation

To solve the motion planning problem, the virtual robot uses A* search on the hypercube lattice.  This searches through the tree of paths starting at the robot’s current position (0,0,0,0) in the lattice until it finds a minimal length route to some point in the lattice whose projection into is less than the specified tolerance away from the destination in .  At each stage, the allowed moves are those edges in the hypercube lattice whose projections do not either leave the “room” the robot is contained in or intersect any obstacles.

A* search also relies on a “heuristic distance”—a way of conservatively estimating distance remaining to to the goal.  This is because the tree of paths is traversed in order of total estimated distance for a given route.  The advantage of this over a  breadth first search, which would in principle also find a minimal solution, is that far fewer paths need to be explored.

An effective heuristic distance in the case of the robot, at least for relatively small problems, comes from again using the projection from to and checking the Euclidean distance to the specified goal.

The big point here is that although the robot’s shortest path between two points in a room might not look to us much like a straight line:

it’s still a minimal path in a 4 dimensional lattice, projected down to the plane.

Real robots

Obviously, my virtual robot is an idealization.  For the real robot it is based on, two kinds of uncertainty come into play: uncertainty in the current configuration, and uncertainty in the moves from one configuration to another.  The planning problem must interact with the “robot localization” problem.

First, there is uncertainty in the robot’s current position and orientation.  For example, even assuming the robot can move with perfect accuracy, optimal planning is very sensitive to errors in angular placement (“attitude”).  If you want to get from (0,0) to (1, 2), and the robot’s placement is very accurate, it will move like a knight:

But rotate its starting position just 2 degrees to the left, and you’ll need 16 moves to get to the same point with an accuracy of ±0.05 m:

Rotate it 2 degrees to the right, and you’ll need 20 moves to get the same accuracy:

Small perturbations in the position of the robot obviously has a similar effect.

More importantly, the moves themselves are not completely accurate.  On the real robot, I had a potentiometer that adjusted the relative speed of the two side wheels to calibrate the forward motion.  Imperfect calibration means not driving in a completely straight line.  Similarly, during a rotation, there was surely also some tiny change in position as well.

When we account for both types of uncertainty, there is a probability distribution for the initial configuration of the robot, including position and orientation.  There is also a probability distribution for the result of each possible rotation or translation move.  Using Bayesian probability, these two distributions are convolved each time we make a move, in order to get the probability distribution for the updated configuration.

The accumulation of errors make accurate motion planning impossible unless we give the robot the ability to “sense” its environment, use sensory data to update its configuration distribution, and adjust the plan accordingly.  But that’s a discussion for another time.

Fractals and Monads – Part 3

I promised more examples of using monads to draw fractals.  Let’s do some!

Today I’ll explain a simple method to draw lots of fractal pictures with minimal code, using the idea of Kleisli powers I introduced in the previous part. This will be easy to implement in Haskell, and accessible even if you’re not a Haskell programmer.

To do this, I’ll first introduce another well known way of drawing fractal pictures, using random motion.  If you haven’t seen this before, it’s cool in its own right, but then we’ll change the rules slightly and generate fractals instead using monads.  I’ll again be using the power set and list monads this time, so if you’ve read the first two parts, this should be familiar.

The Chaos Game

In the “Chaos Game” you pick a fixed set of affine transformations of the plane, usually all contraction mappings, and then watch what happens to a single point in the plane when you apply a randomly chosen sequence from our set of transformations.

For example, in the best-known version of this game we take just three transformations, each a scaling of the plane by a factor of 1/2, but each around a different fixed point. More precisely, fix points A, B, and C, the vertices of a triangle, and define three corresponding transformations 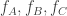by

Here’s how the game typically starts:

I’ve picked a random starting point and a random sequence which begins B, A, C, B, B, B, A, A, B, … .  You can see that at each step, we’re moving in a straight line half way to the next point in the sequence.

At first, it doesn’t sound doesn’t seem like anything very exciting is happening.  But if we keep going, we find something interesting.  To show the pattern more clearly, I’ll stop drawing the lines between steps, and just keep track of the successive points.  I’ll also shrink the dots a little, to avoid them running into each other.  Here’s what a typical random orbit looks like after 3000 iterations:

A picture of the Sierpinski triangle is already emerging.  After 10,000 iterations it looks like this:

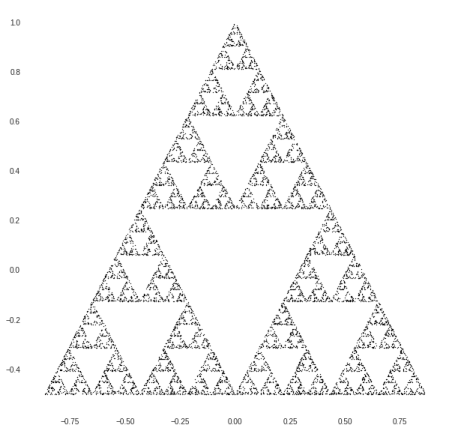
And after 50,000 iterations it’s getting quite clear:

There are tons of variations of the “chaos game,” which also go by the less flashy but more descriptive name of “Iterated Function Systems.”  But let’s get to the monads.

Removing the Randomness with Monads

What does the Chaos Game have to do with monads?  While it’s fun to generate fractal pictures using random motion, we can also trade this random process for a completely  deterministic one in which we iterate a single morphism in the Kleisli category of a monad.

In general, an alternative to making random selections between equally likely steps is to take all of the possible steps simultaneously.  That is, we can get rid of the randomness at the cost of replacing the ordinary functions with a multi-valued function.  Monads give us a nice way to handle this: we’ve seen before that multi-valued functions are just morphisms in the Kleisli category of the power set monad, and we can compose them using Kleisli composition.

In our case, the functions used in the chaos game are 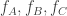, which move points closer to A, B, C, respectively.  We can combine these into a single function

given by

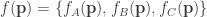
We then have only to iterate this.

The resulting code gives us pictures similar to the ones for the original chaos game, but much more regular and symmetric, since we’ve avoided making any random choices by making all possible choices.  If we also start out in a symmetric state, picking (0,0) as our starting point, and letting the fixed points A, B, and C form an equilateral triangle centered around this point, then at each generation thereafter we get a picture that has all of the symmetries of a triangle.

Here’s generation 6, with 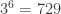points:

Here’s generation 8, with 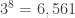points:

And here’s generation 10, with 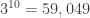points:

Comparing this to the picture from the chaos game with 50,0000 iterations, the two are very similar, though the “monadic” version has sharper edges, and none of the small scale noise of the random version.

The code

To implement this in Haskell, I need to define what a point in the plane is, and define a few operations on points.  I’ll define a new data type, Point, which really just consists of pairs of real (or more accurately, floating point) numbers, and I’ll define vector addition and scalar multiplication on these in the obvious way:

type Point = (Float,Float)

add :: Point -> Point -> Point
add (x1,y1) (x2,y2) = (x1+x2,y1+y2)

mult :: Float -> Point -> Point
mult r (x,y) = (r*x,r*y)

Sure, I could use a linear algebra library instead; I’m implementing these operations myself mainly because it’s easy, and perhaps more friendly and instructive for those new to Haskell.

Using these operations, we can build a function that scales the plane around a given point. I’ll do this more generally than in the examples above, because it will be useful for other versions of the chaos game which I’ll discuss later.  If is a point in the plane, and is a real number, then the function

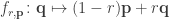
scales 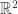by a factor around the point 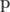. Here’s a Haskell implementation of this function:

scaleAround :: Float -> Point -> Point -> Point
scaleAround r p q = ((1-r) `mult` p) `add` (r `mult` q)

This can be read as saying we take two parameters, a real number r and a point p, and this results in a function from points to points, which is really just .  The ` marks around add and mult let us use these as “infix” operators, as opposed to prefix operators like in Polish notation; for example 3 `mult` (1,0) means the same as mult 3 (1,0), and both give the result (3,0).

Now, we can make a list-valued function that will generate the Sierpinski triangle.  First, let’s fix the vertices of our triangle, which will just be a list of Points:

triVertices = [(sin(2*k*pi/3), cos(2*k*pi/3)) | k <- [0..2]]

This is so much like the mathematical notation for sets that it needs no explanation; just squint until the <- starts to look like 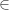, and remember that we’re dealing with Haskell lists here rather than sets.

As before, our function for generating this fractal combines all of the where 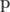ranges over the vertices in the triangle:

f :: Point -> [Point]
f q = [scaleAround 1/2 p q | p <- triVertices]

The first line is the type signature of the function; it just says f takes a point as input, and returns a list of points as output.  This is our morphism in the Kleisli category of the list monad.  The rest of the code just amounts to taking Kleisli powers of this morphism.  Recall that code from last time:

kpow :: Monad m => Int -> (a -> m a) -> a -> m a
kpow 0 _ = return
kpow n f = f <=< kpow (n-1) f

That’s everything we need.  Let’s pick our starting point in to be the origin, set the number of generations to 10, and calculate the output data:

startPt = (0,0) :: Point
nGens = 10

outputData = kpow nGens f $ startPt

The last line here takes the 10th Kleisli power of f, and then applies that to the starting point (0,0). The result is the list of points, and if you plot those points, you get the picture I already posted above:

More examples

Once you know the trick, you can build new versions of the chaos game to generate other fractals.

Here’s a fun one. Before, we started with an equilateral triangle and scaled around each of its vertices by a factor of 1/2; Now let’s take a regular hexagon and scale around each of its vertices by a factor of 1/3.

To build this using our monadic methods, all we really need to change in the code I’ve written above is which vertices and scaling factor we’re using:

hexVertices = [(sin(2*k*pi/6), cos(2*k*pi/6)) | k <- [0..5]]

f q = [scaleAround 1/3 p q | p <- hexVertices]

The result?

It’s a Koch curve!  Or rather, it’s lots of copies of the Koch curve at ever smaller scales. This is just the fractal that I’ve written about before, starting with “Fun with the Koch Snowflake” which I wrote when I first discovered it. It’s like a “Sierpinski Koch snowflake” because it can also be built by starting with a Koch snowflake and the repeatedly removing a Koch snowflake from the middle to leave six new Koch snowflakes behind.

The reason this slightly modified chaos game gives the Sierpinski Koch snowflake is essentially that, at each stage, the Koch snowflake splits into six new Koch snowflakes, each a third of the size of the original, and distributed in a hexagonal pattern.

How does this generalize?  There’s a whole family of fractals like this, which I posted about before, and there’s a version of the chaos game for each one.

I explained in Fun with the Koch snowflake how this replication rule for triangles:

leads to the Sierpinski Koch Snowflake we found above:

Similarly, I explained how this replication rule for squares:

leads to an analogous fractal with octagonal symmetry:

and how this replication rule for pentagons:

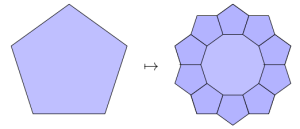
leads to this:

fractal with decagonal symmetry.  This sequence continues.

To get the transformations needed for the chaos game, we just need to calculate how much smaller the polygons get in each successive generation. If you stare at the replication rules above, you can see that pattern I’m using: the edge of the parent polygon is congruent to two edges of the child polygon plus a segment extending from one vertex to the next-to-adjacent vertex of the child polygon.  Solving this, the correct scaling factor is

.

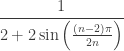The chaos game—and the tamer “monadic” variant on it—for these fractals just amounts to scaling by this factor around each of the vertices in a regular 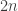-gon.

By the way, you might be tempted (I was!) to include some rotations in addition to the scale transformations, since in the polygon-based versions, only half of the polygons have the same angular orientation as their parent.  However, these rotations turn out not to matter when we’re using points as our basic geometric objects rather than polygons.

Again, there’s little code we need to modify.  First, since we need polygons with any number of sides, let’s make a function that takes an integer and gives us that many vertices distributed around the unit circle, with the first vertex always at 12 O’Clock:

polyVertices :: Int -> [Point]
polyVertices n = [(sin(2*k*pi/nn), cos(2*k*pi/nn)) | k <- [0..(nn-1)]]
    where nn = fromIntegral n

If you’re new to Haskell, this should all be familiar by now, except perhaps the last line. Haskell will complain if you try dividing a floating point number by an integer since the types don’t match, so the integer n has to be converted to a float nn; this makes k also a float, since the notation [0..x] actually means the list of all of the floating point integers from 0 to x, if x is a floating point number, and then everything in sight is a float, so the compiler is happy.

We then have to change our generating morphism to:

f :: Int -> Point -> [Point]
f n q = [scaleAround r p q | p <- polyVertices (2*n)]
    where r = 1/(2 + 2*sin((nn-2)*pi/(2*nn)))
          nn = fromIntegral n

and remember that the generating morphism is now not just f but f n.

Now we can set the starting point, the number of “sides” of the basic polygon, and the number of generations, as we wish:

startPt = (0.2,0.5) :: Point 
m = 5               -- number of generations
n = 7               -- number of "sides"

outputData = kpow m (f n) $ startPt

Just remember that the final list is a list of 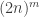points, so don’t blame me if you make these numbers big and run out of memory. :-)

In any case, with code like this, you can generate analogs of the Sierpinski Koch snowflake based on squares:

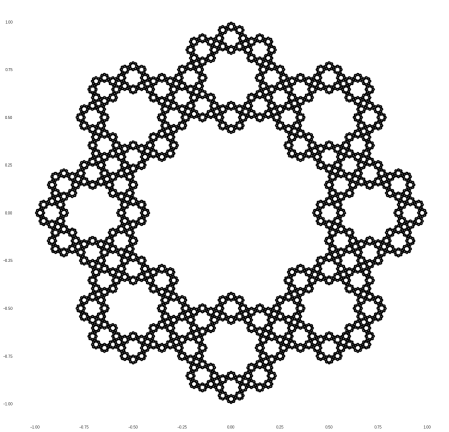
Pentagons, which start “overlapping”:

Hexagons, where the overlapping becomes perfect:

and more.  Heptagons, where the overlapping gets a bit more severe:

Octagons:

and so on.

But enough of that.  Next time, I’ll move on to fractals of a different sort …

Fractals and Monads – Part 2

Last time I discussed the power set monad and how it shows up in certain methods of building fractals.  This time I’ll go a bit further, and also explain some Haskell code I actually use to generate fractal pictures like this:

To do this, I’ll introduce Kleisli categories, the list monad, and a bit about how monads work in Haskell!

Recall we were considering fractals that can be built using a “replication” function

on some set of “shapes” .  As an example, we had considered a map that takes any triangle in the plane to sets of three new triangles as shown here:

and we noted that “iterating” this map indefinitely gives us all of the triangular “holes” in a Sierpinski triangle:

I also described how iterating this map, if we do everything carefully, involves the structure of the power set monad.

In fact, considering maps like leads us directly to the “Kleisli category” associated to the power set monad.  I want to explain this here, because in computer science people actually tend to think of monads essentially in terms of their associated Kleisi categories, and that’s how monads are implemented in Haskell.

Every monad has an associated Kleisli category, but since I’ve been working with the power set monad in the category of sets, I’ll start with that special case.

First, in the Kleisli category, which we’ll denote , the objects are the same as the original category : they’re just sets.  A morphism from the set to the set , however, is a function

For now, at least, I’ll avoid making up any special notation for morphisms in the Kleisli category, and instead freely regard either as a morphism from to in the category of sets, or as a morphism from to in the Kleisli category ; these are really the same thing.  If this is confusing, whenever you’re thinking of as a morphism in the Kleisli category, just think of the as decoration on the arrow , rather than on the codomain object .

Given two functions and , the Kleisli composite is defined by

Checking the domain and codomain of each of the functions on the right, we can see that this indeed gives a morphism from to in the Kleisli category:

You can check that is associative, and that the maps are identity morphisms, so we really do get a category. That’s all there is to the Kleisli category.

Returning to the sort of function we had been considering for generating fractals:

these are clearly just endomorphisms in the Kleisli category.  This also makes it clear what we mean by “iterating” such a function: it’s an endomorphism, so we can just compose it with itself as many times as we want.  In particular, analogously to how we define “powers” of ordinary functions by repeated composition, we can define the nth Kleisli power of recursively by

That is, the 0th power of is the identity, while the nth power of is the Kleisli composite of with its (n-1)st power.

For example, consider the set of all equilateral triangles in the plane and consider the map defined so that has six elements, each 1/3 the size of, and linked together around the boundary of the original triangle , as shown here:

Then, starting with an arbitrary triangle the images under successive Kleisli powers of the generating endomorphism:

look like this:

Some Haskell

Let’s do some Haskell—If you don’t know Haskell, don’t worry; I’ll explain what everything means. If you do know Haskell, this will be super easy, perhaps even obvious, though I may write things in ways you won’t expect, since I’m transitioning over from the categorical definition of monad, rather than diving in with how monads are actually defined in Haskell.

The code we really need is almost embarrassingly short, mainly because monads are extremely well suited to the task at hand.  What we need most is just to be able to compute Kleisli powers!

Here’s how the formula for the Kleisli power of an endomorphism becomes a function in Haskell:

import Control.Monad

kpow :: Monad m => Int -> (a -> m a) -> a -> m a
kpow 0 _ = return
kpow n f = f <=< kpow (n-1) f

Let’s go through this line by line.

The first line just loads some tools for working with monads; there’s not much I need to say about that now.

The next line is the first one of real content; it’s the “type signature” of the function “kpow”.  The first bit, Monad m, just says that m is any monad; Haskell knows about several monads, and you can also define your own.   Then, the rest of that line:

Int -> (a -> m a) -> a -> m a

can be interpreted as declaring that we have a function that takes one integer (Int), the “power,” and one element of , (i.e. something of type a -> m a), and gives us another element of .  So if I were to write this line in standard mathematical notation, I would write:

where is any monad, and is any type.  We take an integer and a Kleisli endomorphism for the monad m, and return another endomorphism. Notice there’s a slight discrepancy here, in that an Int is any integer, whereas I used the natural numbers .  But the integer really is intended to be non-negative.  If you fed a negative integer into kpow, the recursion would never terminate; so, my code doesn’t forbid it, but you shouldn’t do it.

The last two lines of the code give the actual formula for the Kleisli power. If you just look at my earlier formula:

and compare this to these two lines:

kpow 0 _ = return
kpow n f = f <=< kpow (n-1) f

you can probably figure out all of the Haskell syntax just by matching up symbols.

The first line says “whenever the first argument of kpow is 0, the result is “return.” This may be confusing if you’re used to how the keyword “return” is used in many other programming languages. Sorry; it’s not my fault! In Haskell “return” means “ for any object “, where the objects in this case are always data types.

The second line says “the nth Kleisli power of f is the composite of f with the (n-1)st power of f”, just as in the other formula. You probably guessed that the Kleisli composite is written f <=< g in Haskell.

Here’s a dictionary relating the notation I’ve been using to Haskell notation for the same thing:

I didn’t need to use , a.k.a. join explicitly in the definition of Kleisli powers, since it’s already wrapped into the definition of Kleisli composition.

List monad

To do some examples I’ll use the list monad, which is a built-in monad in Haskell. This is very much like the power set monad, since “lists” are like sets in many ways, so I can introduce this pretty quickly. We really just need a very basic idea of how the list monad works.

A “list” of elements of “type” can be written written simply as

for a finite list, or for an infinite list.

Making lists of elements of a given type clearly gives a functor analogous to the power set functor: for any function we get a function that just acts element-wise on lists:

mapping a list of elements of type into a list of elements of type .

Based on what we’ve done with sets, you can probably guess how the two natural transformations in the list monad work, too.

First, any single item can be regarded as a list with only one item on it, so

In Haskell, for example, you could take an element of type Int, say the integer 5, and turn it into a list of integers by using return 5. As long as Haskell has a context to know it is working in the list monad rather than some other monad, this will output [5]. Voilà!

Second, the natural transformation turns lists of lists into lists.  If you’ve got a list of to-do lists, you can always turn it into a single list by first writing down the items on the first list, in order, then continuing with the items on the second list, and so on.

In Haskell, If you enter join [[1,2,3],[4,5]], you’ll get [1,2,3,4,5] as output. That’s .

There’s one noteworthy subtlety, which is that infinite lists are also allowed. So, if you have a list of lists:

[Fun stuff to do, Work to do]

and the first item happens to be an infinite list, then if you try joining these lists up into one in the way I described, you’ll never get to any items on the second list. This is one way in the list monad differs from in the power set monad: In the former, as soon as one of the lists is infinite, everything after that gets thrown away. This last part is not obvious; you certainly could devise ways to join a list of infinite lists together and include all of the items, but that’s not how things work in this monad.

You can easily work out how Kleisli composition works from this, so we’ve now got everything we need.

Cantor set in the List Monad.

Let’s do an example: the Cantor set. I’ll represent closed intervals on the real line by ordered pairs in Haskell. So, when I write (0.3, 1.5), I mean the set . I know, round brackets for closed intervals is weirdly non-standard, but in Haskell, square brackets are reserved for lists, and it’s better to keep things straight.

To generate the Cantor set, all we need is the Kleisli endomorphism in the list monad that describes the general step. This can be defined by a one-line Haskell function:

f (p,q) = [(p, p + (q-p)/3), (q-(q-p)/3, q)]

If we apply this to the unit interval (0, 1), here’s what we get:

[(0.0,0.3333333333333333),(0.6666666666666667,1.0)]

So this works: it’s mapping the closed interval to a list of two closed intervals: and .

Now we can compute any step in the construction of the Cantor set by computing Kleisli powers. Let’s just do one. Once you’ve loaded the function kpow, enter this in Haskell:

kpow 3 f (0,1)

and—kapow!—you’ll get this output:

[(0.0,3.7037037037037035e-2),
 (7.407407407407407e-2,0.1111111111111111), 
 (0.2222222222222222,0.25925925925925924),
 (0.2962962962962963,0.3333333333333333),
 (0.6666666666666667,0.7037037037037037),
 (0.7407407407407408,0.7777777777777778),
 (0.888888888888889,0.9259259259259259),
 (0.962962962962963,1.0)]

Ugly isn’t it? But convert to fractions and you’ll see this is doing just the right thing.

I’ll do more examples in the next post.

Lunar Eclipse

Somehow, no matter how many times I’ve seen it, I’m still excited whenever I get to see this show. Here’s the view from Colorado Springs right now:

Fractals and Monads — Part 1

A while back, I posted a bunch of fractal artwork that I did for fun, based on variations of the Koch snowflake; like this one, for example:

This is composed entirely of equilateral triangles, but it’s just one step in an iterated process leading to a fractal consisting of infinitely many Koch snowflakes at ever smaller scales.

I had a lot of fun coming up with designs like this, but actually I didn’t start out wanting to do new things with the Koch snowflake—that was just a fun tangent.  Originally, I was thinking about monads!

It’s high time I got back to what I was originally working on and explained what these fractals have to do with the “power set monad.”  To do that, I should probably start by explaining what the power set monad is.

For any set the power set is the set of all its subsets.  If you’ve ever studied any set theory, this should be familiar.  Unfortunately, a typical first course in set theory may not go into the how power sets interact with functions; this is what the “monad” structure of power sets is all about. This structure has three parts, each corresponding to a very common and important mathematical construction, but also so simple enough that we often use it without even thinking about it.

Let me finally say what the monad structure of power sets actually is.

First, mapping sets to their power sets is actually a functor:  For any function , there corresponds a function

which sends each element , i.e. each subset , to its image:

.

This makes a functor because the mapping of functions gets along nicely with identity functions and composition.   This functor is the first part of the power set monad.

You might be accustomed to writing the image of the set under simply as , rather than .  But here, we need to be more careful: despite its frequent use in mathematics,  is a notational abuse for which is the proper form.

To motivate the next piece in the power set monad, notice that there’s a strong sense in which is just an extension of , namely, on singleton sets, it essentially “is” :

.

This might make it tempting write for , as sort of “dual” version of the previous abuse of notation, though I don’t think anyone does that.

A better way to express how extends is to introduce the canonical map sending elements of to the corresponding singleton sets:

Then, the previous equation can be written , which is precisely the equation that makes a natural transformation. This natural transformation is the second piece in the monad structure.

Anyone who’s taught elementary set theory can attest that some students have a hard time at first making with conceptual distinction between elements and singleton subsets of a set.  Indeed, conflating the two is a very “natural” thing to do, which is why this is a natural transformation.

The last piece of the power set monad is another natural transformation. Much like , which formalizes a way to think of elements as being subsets, there is a natural transformation that lets us think of sets of subsets as being subsets.  This is given by, for each set , a map:

Here is the power set of the power set of , so an element of it is a sets of subsets of , and we turn this into a single subset by taking the union.

That’s it!  Or, almost.  To form a monad, the data must be compatible in such a way that these diagrams commute:

It’s a simple exercise to check that this is indeed the case.  You can extract the general definition of monad from what I’ve written here: you need an endofunctor on some category, and two natural transformations such that the diagrams analogous to those above commute.

Now let’s come back to fractals:

Many kinds of fractals are created by taking a simple shape, making multiple copies, transforming them somehow—for example, by shrinking or rotating—and then repeating.

For example, here’s one way to build a Sierpinski triangle, or rather its complement, staring from a single triangle and a rule for how triangles should “reproduce”:

If we look closely, we see that this process naturally involves ingredients from the power set monad.

In particular, the basic building block is the self-replication rule that we can write as a function

where is the set of triangles in the plane.  We won’t need an explicit formula for the function, since a picture suffices to explain what it does:

We can get all of the triangular holes in the Sierpinski triangle by “iterating” f. But, what does this mean exactly?  It would be nice if we could just do , but, strictly speaking, this doesn’t parse: we can’t feed a set of triangles into , since this is a function that expects a single triangle as input.

Fortunately, we know the solution to this problem: since , we can’t feed it into , but we can feed it into .  Good so far.

The problem with this is that again doesn’t live in , nor does it live in —it lives in :

It seems we would be doomed to march into ever more deeply-nested sets, were it not for the natural transformation .  Fortunately, using we get

So, now we can see the process of building a fractal as just repeatedly applying this function .

One last problem: What do we apply it to?  We want to apply it to our initial triangle , but that’s an element of , not .  Good thing we can think of this as an element of using the natural transformation !

So, here’s a recipe to build a wide variety of fractals, like some of the ones I’ve posted on this blog:

but also tons of others, using the power set monad:

1. Start with a replication rule on some set of “shapes.”
2. Pick a shape .
3. Feed your initial shape into to get the initial state.
4. Iterate feeding the current state into to get a new state, as many times as you want.

In fact, in calling this a “recipe,” I mean more than just an abstract mathematical recipe: this is essentially how I really drew all of those fractal pictures.  I generated them using Haskell—a functional programming language that knows about monads.  I didn’t use the power set monad, but rather Haskell’s built in “list monad,” which works very similarly.

Dark Energy Survey complete tomorrow

Tomorrow, Dark Energy Survey finishes six years of taking data!

This experiment is intended to help us better understand the nature of Dark Energy, which drives the accelerated expansion of the universe.

Shown here is the Dark Energy Camera, a 520-megapixel digital camera the collaboration used to collect 50TB of data on over 300 million distant galaxies during the last 6 years. It will be exciting to see what findings come from analyzing all those data!

http://news.fnal.gov/2019/01/dark-energy-survey-completes-six-year-mission/

Savitzky-Golay filters

There are often two different but equally important descriptions of a given mathematical process — one that makes it simple to calculate and another that makes it simple to understand.

Savitzky-Golay filters are like that. In digital signal processing, they give nice ways to “smooth” a signal, getting rid of small noisy fluctuations while retaining the signal’s overall shape. There are two ways to think about how they work—one based on convolution and another based on approximation by polynomials. It’s not obvious at first why these give the same result, but working out the correspondence is a fun and enlightening exercise.

Graphic by Cdang: Smoothing of noisy data by the Savitzky-Golay method (3^rd degree polynomial, 9 points wide sliding window).

From the name Savitzky-Golay filter, you might well expect one way to think about Savitzky-Golay smoothing is as a convolutional filter.  Indeed, one general method of smoothing a function is to “smear” it with another function, the “filter,” effectively averaging the function’s value at each point with neighboring values.  In this case, the filter function is given by “Savitzky-Golay coefficients.”  You could look these up, or get them from your math software, but they may look rather mysterious until you work out where they came from.  Why these particular coefficients?

The other way to think of Savitzky-Golay smoothing goes as follows.  Suppose you have a digital signal, which for present purposes is just a continuous stream of real numbers:

Now for each , fit a polynomial to on the points between and ,  and replace by the value of this polynomial at .  This approach involves constructing a new polynomial fit at each point: always a polynomial of same degree, but fit to a different set of points.

Again, these two descriptions are equivalent.  The polynomial fit version is a lot more satisfying, in that I can visualize how the smoothing is working, and understand intuitively why this is a good smoothing method.  On the other hand, you wouldn’t want to calculate it using this method, solving a least-squares polynomial fit problem at each step. For calculations, convolution is much faster.

Why are these equivalent?

The key point that makes doing separate least-squares problems at each point equivalent to doing a simple convolution is that we are dealing with digital signals, with values arriving at regularly spaced intervals.  While the dependent variable of the signal could have any crazy behavior you might imagine, the regularity of the independent variable makes most of the least squares calculation the same at each step, and this is what makes the whole process equivalent to a convolution.

Here’s the correspondence in detail.

First, consider how we construct .  This is based on a least squares fit to the points

Here’s a quick review of how this works.  The idea is to find coefficients such that this polynomial of degree d:

gives the best possible predictions for the values of $f(x)$ in that range.  If , then there will be a polynomial whose graph passes perfectly through all points, but in order to have a smoothing effect, we want .  The problem is then to minimize the total squared error:

We can write this compactly using matrices. First, form the design matrix , a matrix with rows given by

for

For example, if k = 4, and d = 2, will have these entries:

     1   -4   16  -64
     1   -3    9  -27
     1   -2    4   -8
     1   -1    1   -1
     1    0    0    0
     1    1    1    1
     1    2    4    8
     1    3    9   27
     1    4   16   64

Notice that the matrix product , where , then gives a column vector of values for the polynomial :

.

Those are the “predicted” values for , so if we let be the column vector of actual values, then our problem is to find a vector that minimizes

.

The gradient

is zero if and only if the normal equation

holds.  When is invertible, which is always the case if $d<2k$, this has solution

This gives the coefficients .  Now, what about the value of ?

Our smoothed version of , agrees at 0 with our polynomial approximation .  Since we are evaluating the polynomial at zero, we get just the degree-zero term.  In other words, is just the topmost entry in the above solution.  That is,

where is the first standard basis vector of .

We’re almost done!  Notice that the previous equation just says the value of the smoothed function at is a certain linear combination of the values of in a window of length around 0.

More importantly, if we were to go through the same process to construct for other values of , it is clear that, by a simple shift of coordinates, we would get a linear combination with the same coefficients as above.

And that’s convolution!  The general formula for the smoothing is thus

.

Returning to the example I gave above, with , calculating gives approximately

-0.09091   0.06061   0.16883   0.23377   0.25541   0.23377   0.16883   0.06061  -0.09091
 0.07239  -0.11953  -0.16246  -0.10606   0.00000   0.10606   0.16246   0.11953  -0.07239
 0.03030   0.00758  -0.00866  -0.01840  -0.02165  -0.01840  -0.00866   0.00758   0.03030
-0.01178   0.00589   0.01094   0.00758   0.00000  -0.00758  -0.01094  -0.00589   0.01178

so the Savitzky-Golay filter in this case is just the first row:

-0.09091   0.06061   0.16883   0.23377   0.25541   0.23377   0.16883   0.06061  -0.09091

Convolving any signal with this filter has the effect of replacing the value at each point with the value of the best quadratic polynomial fit to the values at that point and its eight nearest neighbors.

Quarks and Antiquarks in the Nucleon

My earliest research in physics was in a particle physics collaboration at FermiLab.  The idea of the experiment I worked on from 1994 to 1997 (FermiLab E866) was to study the nucleon sea—a tiny but turbulent region bubbling with quantum activity inside a proton or neutron, where quark-antiquark pairs can appear for an instant before annihilating each other.

In particular, we made a precise measurement of how often pairs of “up” quarks are produced, relative to how often “down” quarks are produced in the nucleon sea, and showed that there was a statistically significant difference which particle physics theory could not account for.

While I went on to more mathematical and theoretical work, I have colleagues who continued research along these lines, and it’s still nice to look in and see what’s going on in the area I started out in.

Fortunately for me, there’s a nice new review article on the subject of quark-antiquark pairs in the nucleon, written by two of my senior colleagues from E866, Don Geesaman and Paul Reimer:

D. F. Geesaman and P. E. Reimer, The Sea of Quarks and Antiquarks in the Nucleon: a Review, https://arxiv.org/abs/1812.10372

It’s nicely written, and explains the state of the art in sea quark physics from both the experimental and theoretical sides.

Learning Artificial Intelligence

One reason to love being a mathematician is that the mathematical universe is so staggeringly enormous that there’s never a shortage of fun new directions to go in the mathematical sciences.

Recently, I’ve been learning AI, and really enjoying digging into both the mathematical aspects of intelligence and the concrete programming skills for building state-of-the-art systems.  One big help for this has been a two-term Udacity “Nanodegree” that I just completed.

Artificial Intelligence Nanodegree and Specializations

The whole program, which took from January through August 2018, consisted of three parts:

1. Introduction to Artificial Intelligence. This covered a bunch of topics in “classical” AI, largely following Russell and Norvig’s text, Artificial Intelligence: A Modern Approach.
2. Deep Learning and Applications.  This covered the hottest topic in AI these days—using deep neural networks to do machine learning—and a bunch of applications.
3. Specializations:
   • Computer Vision.
   • Natural Language Processing.
   • Voice-User Interfaces.

These courses covered a lot of stuff!  For me, it was a good way to boost my skills quickly and help me catch up on developments and literature in AI.  Some people who are also interested in AI have been asking me about this program, so here’s more about what I did in it, and some evaluation of the Udacity courses.